Geometry is a broad study that includes: 2D or 3D shapes, for example, a circle in two dimensions and a sphere in three dimensions; points and lines in space; angles between lines, arcs or circles; lengths of segments and distances from point to point. In this article, let us see what is the perimeter of a right-angled triangle.
Geometry can be illustrated on paper using graphs. Points, lines, surfaces (in three dimensions), planes (in two dimensions), solids, or volumes are all required to create geometric figures drawn on paper using graphs. A graph is created by drawing points at the intersections of the coordinates with perpendicular axes intersecting. Two coordinates can describe a point: ordered pairs that describe the distance from the origin O to the intersection of the axes. Points, lines, surfaces, and planes are then created by drawing straight lines connecting points; for instance, a line is formed if a point is connected to its neighbour.
In geometry, relationships are formed between shapes for them to be useful in solving problems. Measurement aspects like perimeter are required to find out how large or small something is. The intersection is necessary to find out whether two shapes are the same or different. Similarity means that shapes have similar shapes, which may be useful in problem-solving and building up geometric models.
Speaking of triangles, there are several kinds of triangles. A triangle is the first shape that can be said to be formed when three lines intersect. Right triangles, scalene triangles, isosceles triangles, obtuse triangles, equilateral triangles, acute-angled triangles are different types.
A scalene triangle is a triangle with unequal sides, but the perimeter of a scalene triangle will again be equal to the sum of its three sides. If the third side of the scalene triangle is missing and one angle is known, then the third side can be found using the law of cosines.
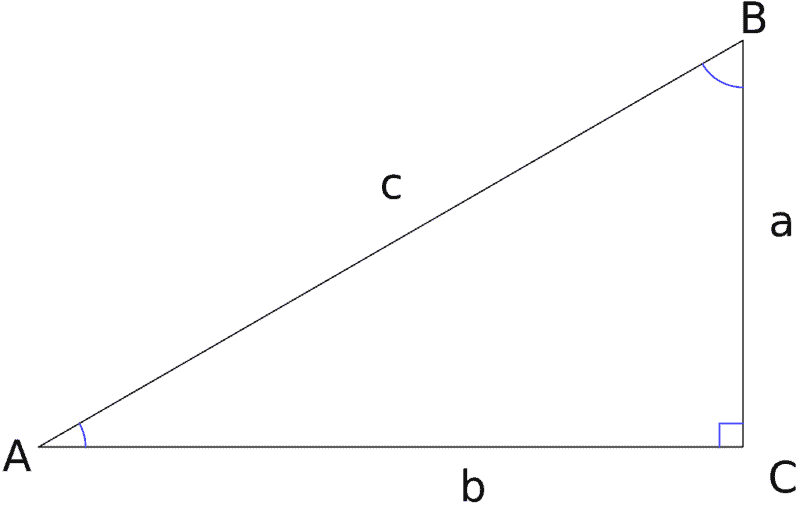
A right-angled triangle is a shape made up of three straight lines that meet at a point. It has a base, an altitude, and a hypotenuse. The base is the side on which the right angle is placed. The altitude is the line drawn from top to bottom of the triangle perpendicular to its base. The hypotenuse is the longest side of the triangle, which lies opposite to its right angle.
A right-angled triangle’s perimeter would be the sum of all three sides; hence the addition of hypotenuse, base, and height would give the periphery of the right triangle. If only two measurements are given for a right-angled triangle, the third can easily be found out using the Pythagoras theorem formula, which states that the sum of the square of the base and the square of the height is equal to the hypotenuse.
For more information on triangles, visit the Cuemath website, which has various study materials on geometry topics. The students can get access to geometry worksheets too for their regular practice. These worksheets are free to download and cover a wide variety of topics. These are great tools for enhancing the student’s creative problem-solving abilities. Also, with the answer keys provided, these worksheets will be a helpful tool in understanding the logic behind problem-solving, thereby increasing students’ overall confidence in dealing with math subjects.
